(Murad Banaji, 13th May 2020)
The numbers of confirmed infections and fatalities in Maharashtra are sufficient to allow some model-based exploration of the COVID-19 outbreak in the state. We use the stochastic, agent-based model previously described (description here, code open sourced on github). The modelling approach involves trying to find model parameters which enable the model simultaneously to explain the infection data and the fatality data for a given outbreak. Computational constraints mean that there is no formal parameter optimisation process at this stage; rather, parameters are chosen using prior knowledge of the dynamics of COVID-19 and mitigation measures, coupled with some attempt to match the time course of infection and fatality data. Fatality rate is a model parameter which can be controlled and which in general cannot be determined from recorded infections and fatalities. Thus we can explore the effects that different fatality rates have on estimates of true infection level – a model output. (See below, and also the analysis for Germany carried out earlier for how this can be carried out).
A slowing in deaths
One notable feature of the Maharashtra data is a rather sudden drop in the rate of increase in deaths which followed a change in protocol in recording COVID-19 deaths by the BMC (Municipal Council of Greater Mumbai) on April 15th 2020. One particular measure adopted as part of this protocol change was to subject each suspected COVID-19 death to an audit before confirming it as such. According to one health official, in “85% of the coronavirus deaths, co-morbidities were responsible and not the infection directly”; this statement and the accompanying arguments suggested strongly that patients with comorbidities might henceforth largely be omitted from the COVID-19 fatality statistics.
The change in protocol appeared to have an immediate effect on the numbers. According to the data available on https://www.covid19india.org/, an average of 18 COVID-19 deaths per day occurred in Maharashtra during each of the five days leading up to 15/04/2020, but this dropped to an average of 9 deaths per day during each of the five days after. This sudden change is also clearly visible in the graph in Figure 1 below.
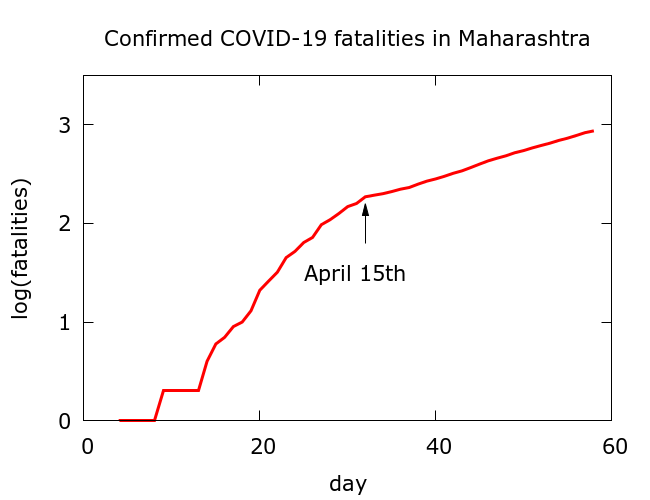
Figure 1. Maharashtra’s COVID-19 fatality data from https://www.covid19india.org/. An immediate drop in the rate of increase of fatalities occurred following the change in protocol for recording COVID-19 deaths in Mumbai on 15/04/2020.
The revision in protocol in Mumbai does not seem to accord with WHO guidelines which, as reported in the Indian Express, define a death due to Covid-19 as one ‘resulting from a “clinically compatible” illness in a probable or confirmed case of Covid-19, “unless there is a clear alternative cause of death that cannot be related” to the disease (for instance trauma).’
It is worth noting that there was no noticeable sudden change in the trajectory of confirmed infections on 15/04/2020, comparable to that visible in the fatalities (see Figure 2 below); although the protocol revision also changed the criteria for COVID-19 testing, this appears to have had no clear impact on the levels of infection being recorded.
Model estimates of lost deaths
Can we estimate the cumulative effect on the total recorded fatalities of the change of criteria for recording COVID-19 deaths? A variety of data driven approaches can be adopted, including simple extrapolation (likely to overestimate deaths), and approaches which use infection-data as a predictor of fatality data. The approach adopted here is similar in spirit to the latter: we use the agent-based model to map the trajectory of the epidemic to date focussing on fitting the reported infections curve. In other words, the underlying assumptions are that:
– the case detection rate has not changed during this period.
– the true fatality rate has not changed during this period.
We will return to these assumptions later. With these assumptions we obtain the model-predicted trajectory of the fatalities and compare this to the observed trajectory. The results of this process for a range of choices of fatality rate are shown in Figure 2.
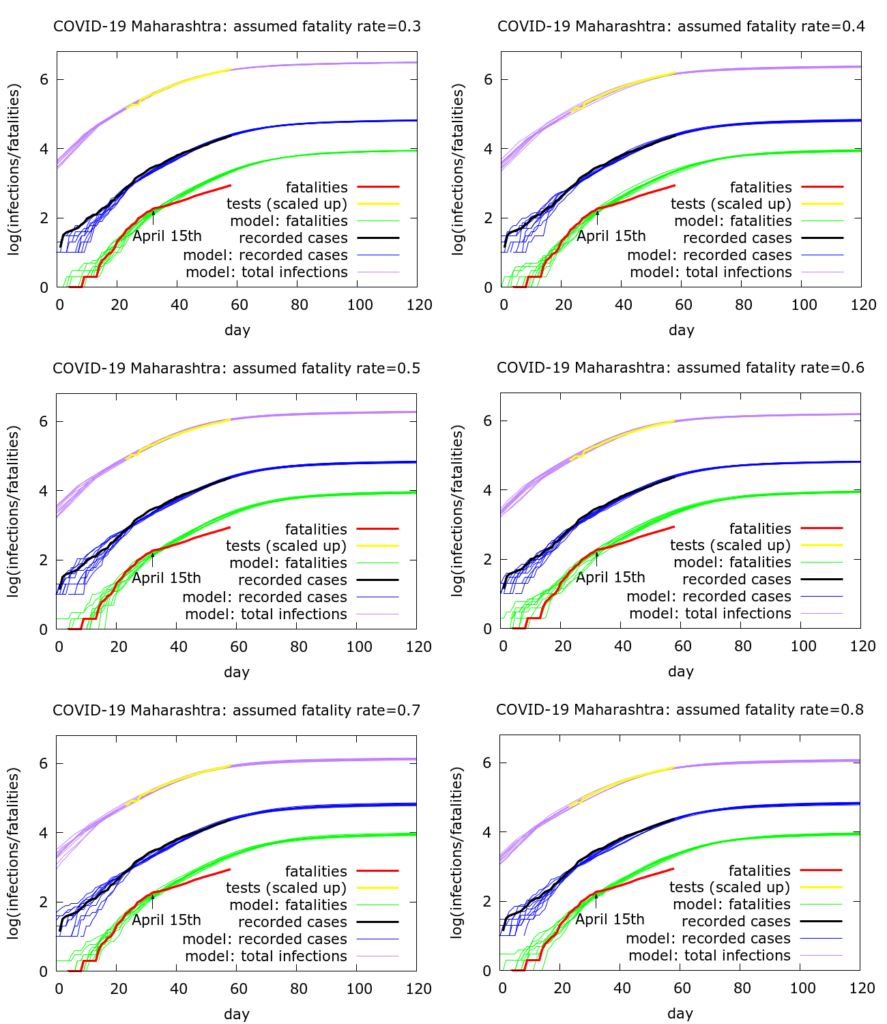
Figure 2 demonstrates a point made earlier that we are able to reproduce the approximate dynamics of the outbreak while varying assumptions on the fatality rate (provided we also vary some other model parameters in a systematic way). The process used to obtain the parameters used in the simulations in Figure 2 is roughly: (i) attempt to model the early dynamics of both infection and fatality data, primarily by exploring the effects of different values of R0 (the basic reproduction number), and the delay between infection reporting and death; (ii) additionally model mitigation so as to explain the infection data through the whole time-course of the epidemic so far. As described previously, mitigation consists of physical distancing which reduces the likelihood of infections occurring, along with localisation of the disease which effectively reduces the available pool of “infectible” people, although there can be some leakage into this pool. The parameters chosen are optimistic, in the sense that it is assumed that mitigation continues to be effective into the future, but of course extrapolation beyond the current date needs to be treated with caution.
Under these assumptions, we can estimate the current (as of 12th May 2020) discrepancy between recorded deaths and modelled deaths. We find model-predicted current total deaths to be between 2000 and 2100, compared to the measured value of 867. Thus, with these assumptions, the model predicts that about 1200 COVID-19 deaths have been “missed”. This prediction is independent of the assumed fatality rate, namely is the same in all the six simulations shown in Figure 2.
Model estimates of total infections
What does change with the fatality rate is the model estimated total infections in Maharashtra. These range from about 700,000 on the assumption of a 0.8% fatality rate to about 1.8 million with a 0.3% fatality rate. Although Mumbai accounts for about 60% of Maharashtra’s total recorded COVID-19 infections (on 12/05/2020), Mumbai’s percentage of Maharashtra’s true infections may be higher: on 15/04 in addition to changing protocols around deaths, testing criteria in Mumbai were changed, possibly leading to under-representation of Mumbai’s contribution to Maharashtra’s infections after this date. Ignoring this effect, and assuming that Mumbai accounts for 60% of Maharashtra’s cases, there would then be between 420,000 and 1.1 million infections in Mumbai as the fatality rate ranges down from 0.8% to 0.3%.
Alternative explanations for the data
We now return to interrogating the validity of the assumptions which led to these estimates. First of all, there are two alternative explanations, other than missing fatalities, that could plausibly be posited for the features of the data mentioned above:
Possibility 1. Testing is capturing an increasing proportion of cases, namely the case detection rate is rising. The slowing in deaths arises from mitigation, but this event is not visible in the testing data as the decrease in cases is offset by higher case detection.
Possibility 2. The fatality rate changed as a consequence of disease spreading in a healthier population with lower likelihood of dying from COVID-19. Testing is picking up a constant fraction of cases, but fewer patients are dying.
Although these alternative explanations could play some part in explaining the data, I have not found convincing evidence for either as the main factor. Regarding possibility 1, as noted earlier, there are no notable features in the testing data at or around 15/04/2020. The “test positivity rate”, namely the ratio of positive tests to total tests has slightly decreased: it stood at 4.7% on April 14th and had dropped to 4.2% on May 12th. This measure is a difficult one to interpret: the drop could be interpreted either as a consequence of wider testing, or as a consequence of less well-focussed testing. But even being generous and assuming that it is a sign that the proportion of infections being picked up by testing has increased, it seems unlikely that this could explain a major part of the discrepancy between the testing and fatality data.
Regarding possibility 2, it is certainly true that infection was surging in new localities – in particular slums – during this period. One can imagine arguments for why this might reduce fatality rate, but this would require some careful work to justify. Poorer communities, while perhaps having a lower average age due to lower life expectancy, may also have a greater number of other underlying health issues placing them at risk of more severe COVID-19 infection. Even if some such demographic factors led to a drop in fatality rate, one would expect this to manifest as a gradual slowing in fatalities.
Conclusions
What can we conclude? Without dismissing possibilities 1 and 2 above, the most plausible explanation for the bulk of the discrepancy developing between infection data and fatality data is unrecorded COVID-19 fatalities as a consequence of a change of protocol. The modelling gives estimates of about 1200 missing fatalities as of 12/05/2020.
One consequence is that estimates of the total levels of infection in Maharashtra are higher than they would otherwise be. At an assumed fatality rate of 0.5% there have been about 1.1 million infections in Maharashtra upto 12/05/2020. Scenarios where the observed fatalities are to be taken at face value and the discrepancy between fatality and testing data springs from an increase in testing or a genuine drop in fatality rate can also be simulated. Some such simulations were presented in earlier work. These would give a somewhat lower total of about 450,000 infections to date.
Appendix
For completeness here are the parameter values used to generate the 6 plots in Figure 2. Note that a scaling was applied to speed up computations: all populations appear at one tenth of their value, and death rates are multiplied by 10.
Figure 2 parameters (subfigures lexicographically ordered)
number_of_runs 10
death_rate 3.0, 4.0, 5.0, 6.0, 7.0, 8.0
geometric 1
R0 4.0
totdays 150
population 1000000
inf_start 3
inf_end 14
time_to_death 17
dist_on_death 6
time_to_recovery 20
dist_on_recovery 6
initial_infections 10
herd 1
percentage_quarantined 2.22, 2.96, 3.7, 4.44, 5.18, 5.92
percentage_tested 100.0
testdate 12
dist_on_testdate 0
haslockdown 1
lockdth -1
lockdown_at_test 7
lockdownlen 150
infectible_proportion 0.1333, 0.1, 0.08, 0.0667, 0.0571, 0.05
pdeff_lockdown 42.0
popleak 3333, 2500, 2000, 1667, 1429, 1250
popleak_start_day 0
physical_distancing 0
pddth -1
pd_at_test 10
pdeff1 80
sync_at_test 100
sync_at_death -1
sync_at_time 26
